Как нарисовать изогнутую стрелку в PowerPoint

19 мая 2015

Стрелки – довольно частый элемент презентации – связи, указатели, ссылки, — всего этого на слайдах хватает. Однако если нарисовать прямую стрелку обычно очень легко, то попытка немного усложнить задачу и добавить к слайду изогнутую стрелку, почти наверняка с первого раза не удастся. Впрочем, учитывая тот факт, что простые, прямые стрелки скучны до безобразия, нам придется что-то придумать.

К счастью, есть очень просто рецепт, которым я с вами сейчас поделюсь.

Основа для стрелки

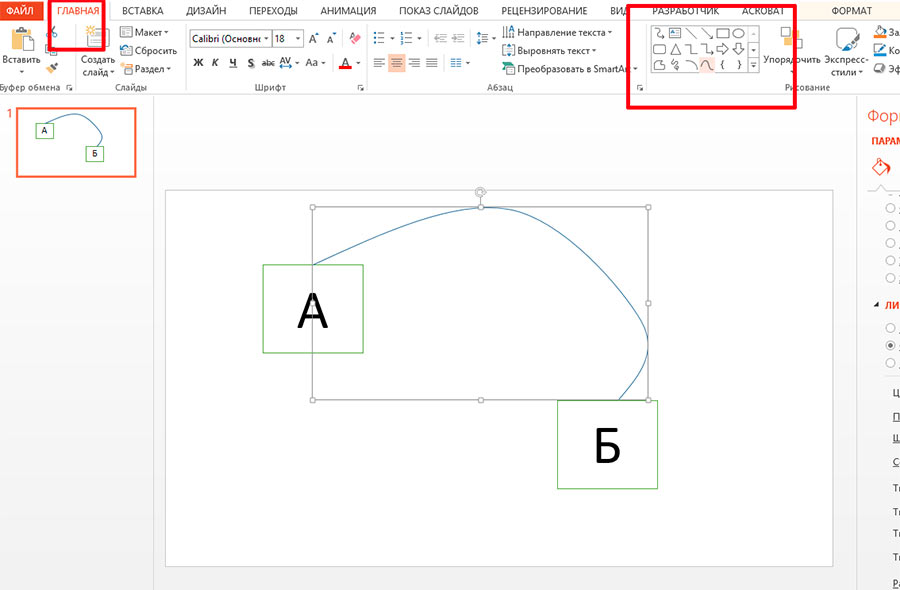
Первым делом добавим контур нашей супер-стрелки, для этого в группе «рисование» на панели «Главная» выберем инструмент «Кривая». По сравнению с другими инструментами этой группы, «кривая» строится по принципу кривых Безье – с каждым щелчком мыши по слайду, на экране будет возникать не кратчайший путь от точки к точке, а плавный, точно выверенный маршрут. Как только кривая будет доведена до конца – нажмите «Esc», чтоб зафиксировать её положение. Если вышло совсем не так ровно, как хотелось – не страшно, сейчас мы это исправим.

Нарисую в PowerPoint два блока и соединю их кривой

Придаем стрелке форму.

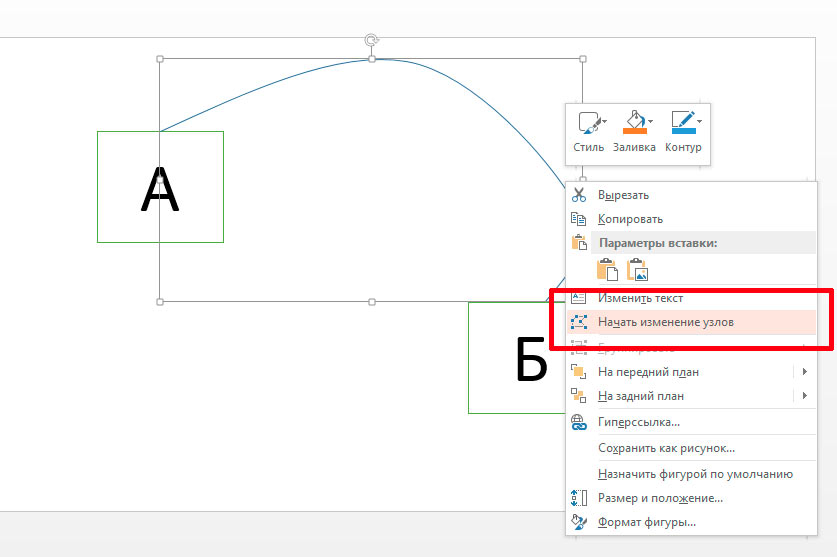
Выделяем нашу кривую, нажимаем на ней правой кнопкой мыши и выбираем в контекстном меню пункт «Начать изменение узлов». Линия изменит цвет, а узловые точки (места, где мы щелкали мышью) станут вновь активными. Перемещая узловые точки, придадим кривой аккуратный, ровный вид.
Обратите внимание: при выборе узловой точки, повторный вызов контекстного меню правой кнопки мыши, выведет ряд дополнительных настроек (добавление, удаление узловых точек, изменение их свойств).

А теперь, займемся кривыми Безье

Заканчиваем создание стрелки

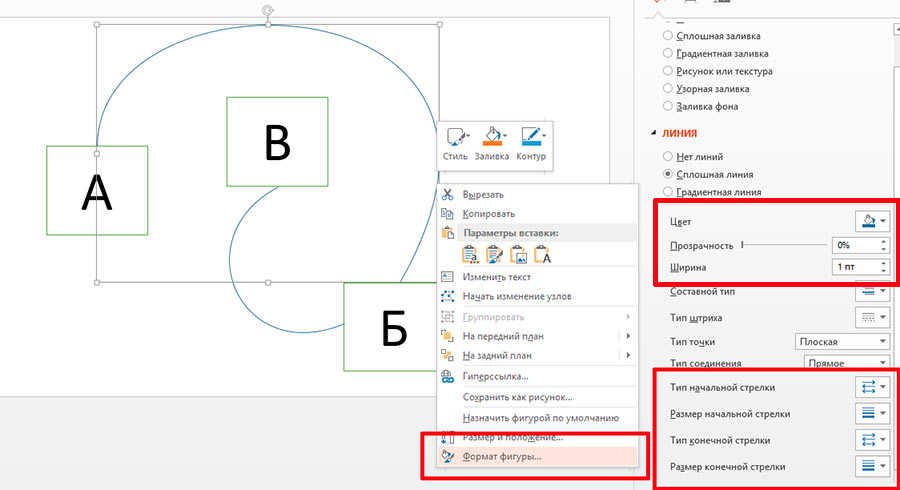
У наших кривых кое-чего не хватает, верно? Придадим им более соответствующий вид: выделяем кривую, нажимаем на ней правой кнопкой мыши и выбираем в контекстном меню пункт «Формат фигуры». В появившемся окне настроек, нас интересуют в первую очередь пункты «Тип конечной стрелки» и «Размер конечной стрелки» — они определяющие «навершие» нашей кривой.

Я немного дорисовал исходный рисунок. теперь превратим кривые в полноценные стрелки.

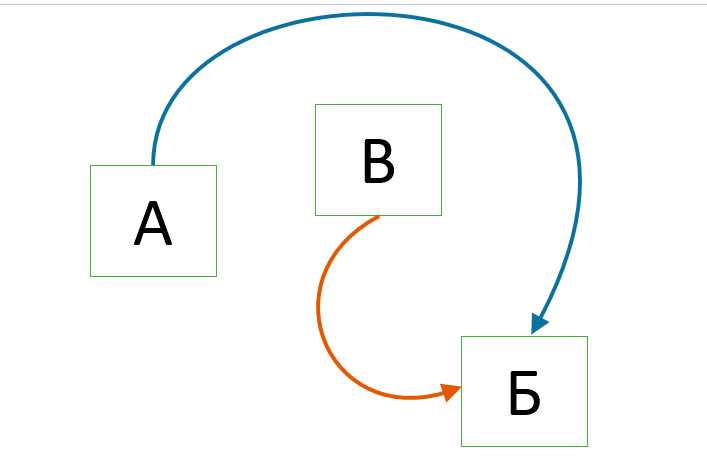
После того, как все встанет на свои места, можно дополнительно визуализировать наши стрелки. Для примера, я раскрасил их разными цветами («Цвет») и задал разную толщину – по степени важности («Ширина»).